个人觉得成熟的rebole的工具 不太适合萌新 来操作自己对于项目的建设
最近找了一个新的项目 来操作
感觉本项目 更贴近萌新到大佬写代码过程 于是乎 有了这篇指南
embedding操作
0. 官方操作
下面是官方例子
1 | import torch |
官方的解释:
torch.nn.``Embedding(num_embeddings, embedding_dim, padding_idx=None, max_norm=None, norm_type=2.0, scale_grad_by_freq=False, sparse=False, _weight=None, device=None, dtype=None)
- num_embeddings:嵌入字典的大小(词的个数);
- embedding_dim:每个嵌入向量的大小;
- padding_idx:若给定,则每遇到 padding_idx 时,位于 padding_idx 的嵌入向量(即 -padding_idx 映射所对应的向量)为0;
- max_norm:若给定,则每个大于 max_norm 的数都会被规范化为 max_norm;
- norm_type:为 max_norm 计算 p-范数的 p值;
- scale_grad_by_freq:若给定,则将按照 mini-batch 中 words 频率的倒数 scale gradients;
- sparse:若为 True,则 weight 矩阵将是稀疏张量。
1. 自己的瞎吉儿理解
这里呀 就只需要理解好 前三个就好
- 对于前两个的理解
torch.nn.Embedding 的权重为 num_embeddings * embedding_dim 的矩阵,例如输入10个词,每个词用3为向量表示,则权重为10*3的矩阵;
- 对于 padding_idx 理解
1 | import torch |

可以看出 “6” 所对应映射的向量被填充了0。
网络初始化
https://blog.csdn.net/dss_dssssd/article/details/83959474
1. 初始化函数
均匀分布
torch.nn.init.uniform_(tensor, a=0, b=1)
服从~U ( a , b ) U(a, b)U(a,b)正太分布
torch.nn.init.normal_(tensor, mean=0, std=1)
服从~N ( m e a n , s t d ) N(mean, std)N(mean,std)初始化为常数
torch.nn.init.constant_(tensor, val)
初始化整个矩阵为常数valXavier
基本思想是通过网络层时,输入和输出的方差相同,包括前向传播和后向传播。具体看以下博文:
为什么需要Xavier 初始化?
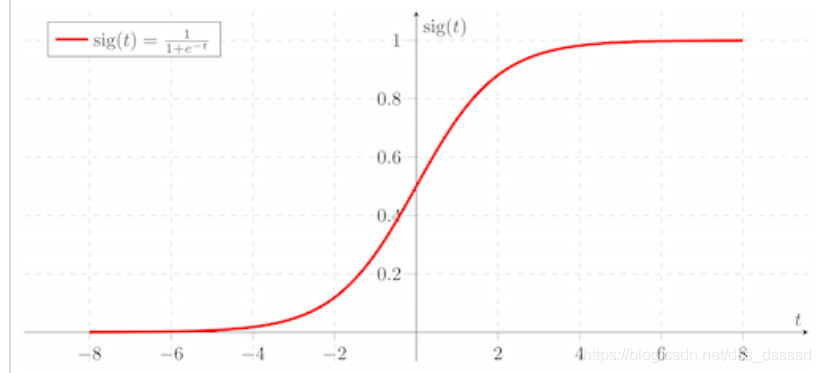
如果初始化值很小,那么随着层数的传递,方差就会趋于0,此时输入值 也变得越来越小,在sigmoid上就是在0附近,接近于线性,失去了非线性
如果初始值很大,那么随着层数的传递,方差会迅速增加,此时输入值变得很大,而sigmoid在大输入值写倒数趋近于0,反向传播时会遇到梯度消失的问题xavier初始化的简单推导
- kaiming (He initialization)
以后再说 现在没用上
bug解决
感谢涛哥 对于源码的修改
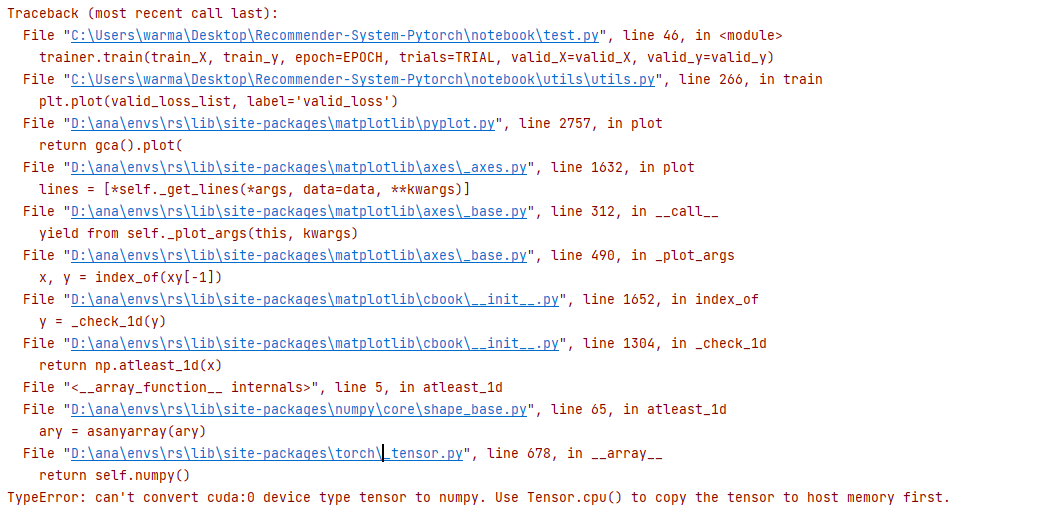
错误信息
在改错的时候注意看最后一行 即
修改
在这里定位好 然后修改成:
1 | return self.cpu().numpy() |